B-Tree
B-tree是一種高效的資料結構,特別適用於處理大量資料和優化I/O操作。它常用於多存儲系統中,特別是磁盤存儲和數據庫系統,以確保高效的數據組織和查詢。
磁碟存取資料:
- 磁碟存取資料的基本過程
- 根據磁柱號碼使磁頭移動到所需要的柱面上, 這一個過程被稱為定位或是查找
- 根據磁盤面號來確定指定盤面上的磁道
- 盤面確定以後, 盤面開始旋轉, 將指定磁區的磁軌段移動至磁頭下
- 磁碟讀取資料是以block為基本單位的, 因此儘量將相關資訊存放在同一個磁區, 同一磁軌中, 以便在讀寫資料時儘量減少磁頭來回移動的次數, 避免過多的查找時間.
- 當大量的資料儲存在磁碟中時, 如何高效地查詢磁碟中的資料, 就需要一種合理高效的資料結構了
使用時機
檔案系統或著是資料庫為了增加搜尋的效率, 就可以採用此資料結構. 在資料量變大時, 若用線性搜尋檔案中的紀錄, 效率其實是不好的, 所以這時候就可以建立索引(index), 但資料量又再度增加時, index檔案也會變得很龐大. 為此, 需要一個有效率的搜尋索引, 才能有效率的找到結果.
B-Tree 特性
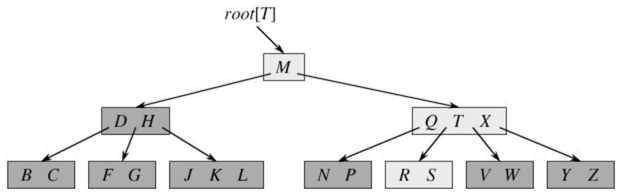
對於一顆m階(階指的是子節點的最大數目)的B-Tree,有如下特性:
- 根節點要麼是葉子,要麼至少有兩個子節點
- 每個節點最多含有m個子節點(m ≥ 2)
- 除了根節點和葉節點之外,其他每個節點至少有⌈m/2⌉個子節點
- 所有的葉節點都出現在同一層上
- 有s個子節點的非葉節點具有n = s - 1個關鍵字,即s = n + 1
- 每個非葉節點中包含n個關鍵字資訊:(n, C₀, K₁, C₁, K₂, C₂, …, $K_n$, $C_n$),其中:
- $K_i$(i = 1…n)為關鍵字,且關鍵字按升序排序:$K_{i-1}$ < K_i
- C_i為指向子樹根的指標,且指標$C_{i-1}$指向的子樹中所有節點的關鍵字均小於$K_i$,但都大於$K_i$
- 關鍵字的個數n必須滿足:$⌈m/2⌉ - 1 ≤ n ≤ m - 1$
B-Tree的高度:
- 就是B-Tree不包含葉節點的層數
- 由於磁碟存取時的I/O次數, 與B樹的高度成正比, 高度越低, I/O次數也就越小, 因此理解如何計算B-Tree的高度是很有必要的
- 假設若B-Tree總共包含N個關鍵字, 則此樹的葉節點可以有N+1個, 而所有的葉節點都在第K層, 可以得出:
- 因為根至少有兩個子節點, 因此第二層至少有兩個節點
- 除了根和葉之外, 其它節點至少有ceil(m/2)個子節點
- 因此在第3層至少有2*ceil(m/2)個節點
- 在第4層至少有2*(ceil(m/2)^2)個節點
- 在第k層至少有2*(ceil(m/2)^(k-2))個節點, 於是有: N+1 ≥ 2*(ceil(m/2)^(K-2)), 這就可以算出: K ≤ log(ceil(m/2))((N+1)/2)+2
- 由於計算B-Tree高度是不包含葉節點的層數, 所以B-Tree的高度 ≤ log(ceil(m/2))((N+1)/2) + 1
本部落格所有文章除特別聲明外,均採用CC BY-NC-SA 4.0 授權協議。轉載請註明來源 YouChen's Blog!